Question

Write an equation of the line that passes through (- 5, - 1) and is perpendicular to the line y=4x-6.

Answer 1

-7

Explanation:

find the gradient of (-5,-1)

Answer 2

`\LARGE\sf{y\:=\:-(1)/(4)x\:-(9)/(4)}`

Explanation:

Given the point, (-5, -1), and the linear equation, y = 4x - 6:

Definitions:

Perpendicular lines:

In order to find the equation of the line that is perpendicular to the given linear equation, we must first define what perpendicular lines are.

By definition, perpendicular lines have negative reciprocal slopes. This means that multiplying the slopes of both equations results in a product of -1: ⇒ m₁ × m₂ = -1

Slopes of Perpendicular Lines:

If the slope of the given linear equation, y = 4x - 6 is m₁ = 4, then it means that the slope of the other line must be m₂ = -¼.

• m₁ × m₂ = -1

• 4 × -¼ = -1

Solution:

Using the given point, (-5, -1), and the slope of the other line, m₂ = -¼, substiute these values into the slope-intercept form: y = mx + b, and solve for the value of the y-intercept, b:

y = mx + b

-1 = -¼(-5) + b

`\LARGE\sf{-1\:=\:-(1)/(4)(-5)\:+\:b}`

`\LARGE\sf{-1\:=\:(5)/(4)\:+\:b}`

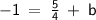
Subtract
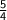`\LARGE\sf{(5)/(4)}` from both sides to isolate b :

`\LARGE\sf{-1\:-(5)/(4)\:=\:(5)/(4)\:-(5)/(4)\:+\:b}`

`\LARGE\sf{-(9)/(4)\:=\:b}`

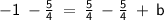
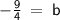
Equation of the Perpendicular Line:

Therefore, the equation of the line perpendicular to y = 4x - 6 is:

`\LARGE\sf{y\:=\:-(1)/(4)x\:-(9)/(4)}`.