Question

The base of a triangle exceeds the height by 7 feet. If the area is 114 square feet, find the length of the base and the height of

the triangle

Answer 1

Height of the triangle = 12 feet

Base of the triangle = 19 feet

Explanation:

Let the height of the triangle be x feet

-> Base of the triangle = (x + 7) feet

`A(\triangle)= 114\: ft^2`

`\because A(\triangle)=(1)/(2)(base)(height)`

`\implies 114=(1)/(2)(x+7)(x)`

`\implies 114* 2= x^2+7x`

`\implies 228= x^2+7x`

`\implies x^2+7x-228=0`

`\implies x^2+19x-12x-228=0`

`\implies x(x+19)-12(x+19)=0`

`\implies (x+19)(x-12)=0`

`\implies (x+19)=0,\:\:(x-12)=0`

`\implies x =-19,\:\:x=12`

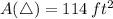
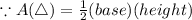
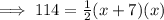
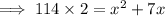
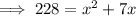
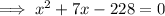
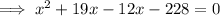
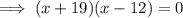
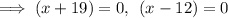
x represents the height of the triangle.

-> x can not take negative value.

`\implies x\\eq -19`

`\implies x = 12`

`\implies x +7= 12+7=19`

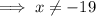
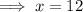
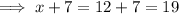
Thus,

Height of the triangle = 12 feet

Base of the triangle = 19 feet