Answer:
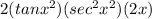
Explanation:
Quick reminder: since
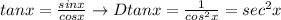
At this point, It's nested function over nested function over nested function, with the most internal one being the quadratic
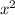 , then the tangent, and then, most external one, it's the tangent squared.
, then the tangent, and then, most external one, it's the tangent squared.
Chain rule. The derivative of the outermost function is

Can you write it in a better form? Maybe. Is it needed? Honestly no.