Question

Am I right??? Please help me

Answer 1

Vertex and y-intercept (0, -5)

x-intercepts (-1.58, 0) (1.58, 0)

opens upwards

other plot points: (-2, 3) (-1, -3) (1, -3) (2, 3)

Explanation:

The graph is not quite correct - it's a little too narrow and doesn't go through the points on the graph.

The y-intercept is when x = 0:

f(0) = 2(0)² - 5

= - 5

Therefore, the y-intercept is at (0, -5)

We also know that the y-intercept is the vertex since the equation is in the form
`f(x)=ax^2+c`

The x-intercepts are when f(x) = 0:

`\implies 2x^2 - 5 = 0`

`\implies x^2 =\frac52`

`\implies x=\pm1.58113883...`

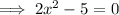
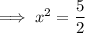
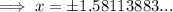
As the leading coefficient is positive, the parabola opens upwards.

Finally, input values -2 ≤ x ≤ 2 to find plot points:

(-2, 3)

(-1, -3)

(0, -5)

(1, -3)

(2, 3)

Answer 2

Function: y = 2x²-5

Find y-intercept:

y = 2(0)²-5

y = -5

Find x-intercept:

2x²-5 = 0

2x² = 5

x² = 2.5

x = ±√2.5

x = -1.5811 , 1.5811

Graph plotted: