Question

Given: △ABC, m∠A=60°,

m∠C=45°, AB=9
Find: Perimeter of △ABC,
Area of △ABC
Pleas be sure to answer BOTH PARTS ... thank you!

Answer 1

p = 32.317

A = 47.911

Explanation:

given ∠A = 60

∠C = 45

AB = 9

From sum of all angles in triangle is 180

∠A + ∠B + ∠C = 180

60 + ∠B + 45 = 180

∠B = 180 - 105 = 75

∠B = 75

from sine rule in ΔABC

AB / sin C = BC / sin A

=> 9 / sin 45 = BC / sin 60

=> 9 / 1/
`√(2)` = BC /
`√(3) / 2`

=>
`9√(2) = BC * 2 / √(3)`

BC =
`9√(2) * √(3) / 2\\`

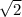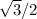
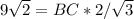
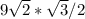
BC = 11.023

length of AC is

AC / sin B = AB / sin C

AC / sin 75 = 9 / sin 45

AC = 9 / 1/
`√(2) * sin 75`

=
`9√(2) * sin 75\\12.294`

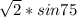
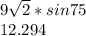
perimeter of ΔABC

AB + BC + CA

= 9 + 11.023 + 12.294

= 32.317

Area of ΔABC is

= 1/2 * AB * AC * sin A

= 1/2 * 9 * 12.294 * sin 60

= 1/2 * 9 * 12.294 * √3/2

= 47.911