Question

Y=1/2x+4
y=-2x+9
elmantion or substutuion method

Answer 1

(2;5)

Explanation:

Elimination:

Let's first multiply the first by 2 to clear fractions and write them both in standard form:

`\left\{ {x-2y=-8} \atop {2x+y=9}} \right. \\`

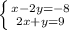
Eliminate x: Multiply the first by 2, then subtract the equations:

`2I-II: 2x-4y-2x-y=-16-9\\-5y=-25 \rightarrow y= 5`

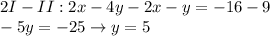
Eliminate y: Multiply the second by 2, then add equations:

`I+2II: x-2y +4x+2y = -8+18\\5x=10 \rightarrow x=2`

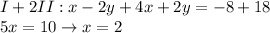
Subtsitution

Solve the first for y (oh, what a coincidence, it's done already!) and replace the value in the second.

`\frac12x +4 = -2x+9 \rightarrow \ x+8=-4x+18\\x+4x = 18-8 \rightarrow 5x=10 \rightarrow x=2`

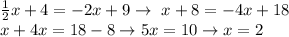
Then let's plug this value into a convenient one - let's say, the first - and find y from there:

`y=\frac12\cdot 2 +4\rightarrow y =1+4 \rightarrow y=5`

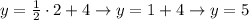
If anyone tries saying it's not substitution, bring the system in standard form, as you did for the elimination method, then solve again for y.