Question

Tìm m để phương trình có 1 nghiệm duy nhất
x+2y-2z=2
3x+7y-z=5
2x+4y+mz=7

Answer 1

Rewrite the system of equations in matrix form.

`\begin{bmatrix}1&2&-2\\3&7&-1\\2&4&m\end{bmatrix} \mathbf x = \mathbf b`

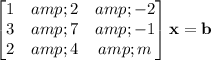
This system has a unique solution
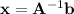`\mathbf x = \mathbf A^(-1)\mathbf b` so long as the inverse of the coefficient matrix
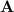`\mathbf A` exists. This is the case if the determinant is not zero.

We have

`\det(\mathbf A) = m+4`

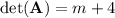
so the inverse, and hence a unique solution to the system of equations, exists as long as m ≠ -4.