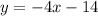Explanation:
Formulas and Formats we'll be using:
Slope Formula:
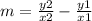
Slope-Intercept form:
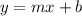
m = slope
b = y-intercept
Substitute (-6, 10) and (-3, -2) into the slope formula:
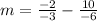
Simplify:
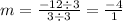
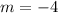
*Per every -4 y, x increases by 1.
Points Included:
(-6, 10)
(-5, 6)
(-4, 2)
(-3, -2)
(-2, -6)
(-1, -10)
(0, -14)
Y-intercept:
Y-intercept represents x when it's equal to 0.
Using our points, we can determine that the y-intercept is at the point:
(0, -14)
-14 is the y-intercept.
Create a Slope-intercept form equation:
Formula:
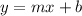
Substitute the slope, and y-intercept into the equation:
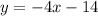
Your equation is: