Question

Hello help me with this question thanks in advance​

Answer 1

`\bold{\huge{\underline{ Solution \:1}}}`

• Yes, ΔEDF and ΔBCA are similar

If we look at the both the triangles then the

• 
  `\sf{ {\angle} E = {\angle}B }`
• 
  `\sf{ {\angle} F = {\angle}A }`

From above, we can conclude that :-

Both the triangles are similar by AA Similarity

Hence, Option A is correct.

`\bold{\huge{\underline{ Solution \:2}}}`

Let consider the given triangle be ABC and the line that divides the triangle consider it as DE

• Here, DE || BC

So,

• 
  `\sf{( AD )/( AB )}{\sf{ = }}{\sf{(AE)/(AC)}}{\sf{=}}{\sf{(DE)/(BC)}}`

Therefore,

• ΔABC similar to ΔADE by SSS congruence similarity criterion.

Now,

We have to find the value of x

In ΔABC, By using BPT theorem

• If the line is drawn parallel to one side of the triangle which intersect the other two sides at specific points then the other two sides are in proportion .

That is,

`\sf{( AD )/( AB )}{\sf{ = }}{\sf{(DE)/(BC)}}`

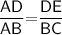
Subsitute the required values,

`\sf{( 6 )/( 6 + 4 )}{\sf{ = }}{\sf{(8)/(x)}}`

`\sf{( 6 )/( 10 )}{\sf{ = }}{\sf{(8)/(x)}}`

`\sf{( 3 )/( 5 )}{\sf{ = }}{\sf{(8)/(x)}}`

`{\sf{ x = 8{*} }}{\sf{(5)/(3)}}`

`{\sf{ x = }}{\sf{(40)/(3)}}`

`{\sf{ x = 13}}{\sf{(1)/(3)}}`

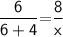
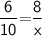
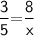
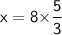
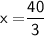
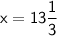
Hence, Option C is correct

`\bold{\huge{\underline{ Solution \:3}}}`

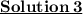
Here,

• SRT similar to BAC

For x,

By using BPT theorem,

`\sf{( AB )/( RS )}{\sf{ = }}{\sf{(BC)/(ST)}}`

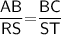
Subsitute the required values,

`\sf{( 2 )/( 4 )}{\sf{ = }}{\sf{(x)/(6)}}`

`\sf{( 1 )/( 2 )}{\sf{ = }}{\sf{(x)/(6)}}`

`\sf{ x = }{\sf{(6)/(2)}}`

`\sf{ x = 3 }`

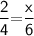
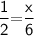
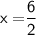
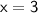
Thus, The value of x is 3

For y

Again by using BPT theorem,

`\sf{( AB )/( RS )}{\sf{ = }}{\sf{(AC)/(RT)}}`

Subsitute the required values,

`\sf{( 2 )/( 4 )}{\sf{ = }}{\sf{(5)/(y)}}`

`\sf{( 1 )/( 2 )}{\sf{ = }}{\sf{(5)/(y)}}`

`\sf{ y = 5{*}2 }`

`\sf{ y = 10 }`

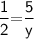
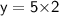
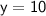
Thus, The value of y is 10

Hence, Option A is correct.