Question

`\sf \lim_(x \to \infty) \cfrac{√(x-1)-2x }{x-7}`

Answer 1

Answer: -2

======================================================

Work Shown:

`\displaystyle L = \lim_(x\to\infty) ( √(x-1)-2x )/( x-7 )\\\\\\\displaystyle L = \lim_(x\to\infty) ( (1)/(x)\left(√(x-1)-2x\right) )/( (1)/(x)\left(x-7\right) )\\\\\\\displaystyle L = \lim_(x\to\infty) ( (1)/(x)*√(x-1)-(1)/(x)*2x )/( (1)/(x)*x-(1)/(x)*7 )\\\\\\`

`\displaystyle L = \lim_(x\to\infty) \frac{ \sqrt{(1)/(x^2)}*√(x-1)-2 }{ 1-(7)/(x) }\\\\\\\displaystyle L = \lim_(x\to\infty) \frac{ \sqrt{(1)/(x^2)*(x-1)}-2 }{ 1-(7)/(x) }\\\\\\\displaystyle L = \lim_(x\to\infty) \frac{ \sqrt{(1)/(x)-(1)/(x^2)}-2 }{ 1-(7)/(x) }\\\\\\\displaystyle L = ( √(0-0)-2 )/( 1-0 )\\\\\\\displaystyle L = (-2)/(1)\\\\\\\displaystyle L = -2\\\\\\`

-------------------

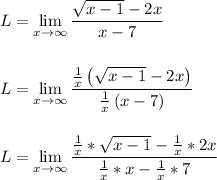
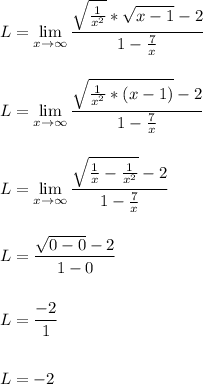
Step-by-step explanation:

In the second step, I multiplied top and bottom by 1/x. This divides every term by x. Doing this leaves us with various inner fractions that have the variable in the denominator. Those inner fractions approach 0 as x approaches infinity.

I'm using the rule that

`\displaystyle \lim_(x\to\infty) (1)/(x^k) = 0\\\\\\`

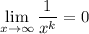
where k is some positive real number constant.

Using that rule will simplify the expression greatly to leave us with -2/1 or simply -2 as the answer.

In a sense, the leading terms of the numerator and denominator are -2x and x respectively. They are the largest terms for each, so to speak. As x gets larger, the influence that -2x and x have will greatly diminish the influence of the other terms.

This effectively means,

`\displaystyle L = \lim_(x\to\infty) ( √(x-1)-2x )/( x-7 ) = \lim_(x\to\infty) ( -2x )/( x) = -2\\\\\\`

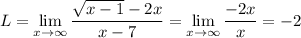
I recommend making a table of values to see what's going on. Or you can graph the given function to see that it slowly approaches y = -2. Keep in mind that it won't actually reach y = -2 itself.