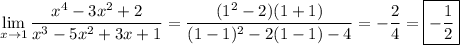Without using L'Hopital's rule:
Factorize the numerator.

Factorizing cubics is usually a bit trickier. But we know x = 1 makes the denominator vanish, so x - 1 is a factor of the cubic. So for some constants a and b,
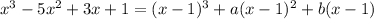
Expanding the right side gives
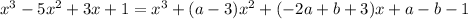
Then
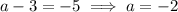
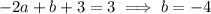
So we rewrite the limit as
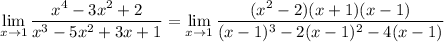
x is approaching 1 so x ≠ 1 and we can cancel out factors of x - 1 :
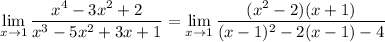
The simplified limand is continuous at x = 1, so we can now evaluate the limit by direct substitution.