Explanation:

Given integral is
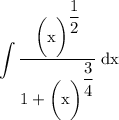
To evaluate this integral, we have to first remove the fractional exponents from the integrand.
So, we substitute
![\sf{x = {y}^(4) \: \: \: \: \: \: \: \: \: \: \bigg[\rm\implies \:y = {\bigg(x\bigg) }^{(1)/(4) }\bigg] }](https://img.qammunity.org/2022/formulas/mathematics/college/v09qddu579dcv30e1y24fwzn6r66onx31p.png)
So, on substituting these values, above integral can be rewritten as
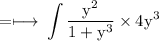
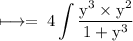
To evaluate this integral further, we substitute
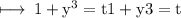
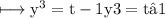
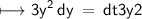
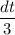
So, on substituting these values in above integral, we get
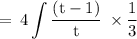
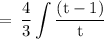
![\rm \: = \: (4)/(3) \displaystyle\int\rm \bigg[1 - (1)/(t) \bigg] \:](https://img.qammunity.org/2022/formulas/mathematics/college/8ogaeb2iisxtcurj4w37fwth7jvueqrp69.png)
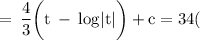
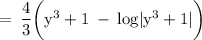
![\rm \: = \: (4)/(3) \bigg[ {\bigg(x \bigg) }^{(3)/(4) } + 1 \: - \: log \bigg| {\bigg(x\bigg) }^{(3)/(4) } + 1\bigg|\bigg] \:](https://img.qammunity.org/2022/formulas/mathematics/college/94qg1g2piakxf62rs5guewwftyigwhjz2l.png)
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
ADDITIONAL INFORMATION
