Question

`\rm\int_(0)^{ (\pi)/(2) } \cot(x) \ln(\sec(x)) \\`​

Answer 1

Substitute y = tan(x) and dy = sec²(x) dx to transform the integral to

`\displaystyle \int_0^(\frac\pi2) \cot(x) \ln(\sec(x)) \, dx = \frac12 \int_0^\infty (\ln(1+y^2))/(y(1+y^2)) \, dy`

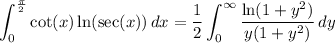
and we split the integral at y = 1.

Examining the one over [0, 1], expand into partial fractions :

`\frac1{y(1+y^2)} = \frac1y - \frac y{1+y^2}`

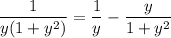
Then

`\displaystyle \int_0^1 (\ln(1+y^2))/(y(1+y^2)) \, dy = \int_0^1 \frac{\ln(1+y^2)}y \, dy - \int_0^1 (y \ln(1+y^2))/(1 + y^2) \, dy`

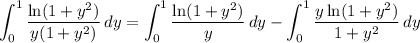
In the integral over [1, ∞), substitute y = 1/z :

`\displaystyle \int_1^\infty (\ln(1+y^2))/(y(1+y^2)) \, dy = \int_0^1 \frac{z \ln\left(1+\frac1{z^2}\right)}{1+z^2} \, dz \\\\ = \int_0^1 (z \ln\left(1+z^2\right))/(1+z^2) \, dz - 2 \int_0^1 (z \ln(z))/(1+z^2) \, dz`

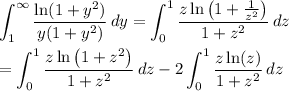
Some terms cancel and we're left with

`\displaystyle \int_0^\infty (\ln(1+y^2))/(y(1+y^2)) \, dy = \frac12 \int_0^1 \frac{\ln(1+y^2)}y \, dy - \int_0^1 (y \ln(y))/(1+y^2) \, dy`

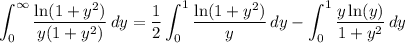
Use the series expansions of ln(1 + y) and 1/(1 - y) - both are valid for |y| < 1.

`\displaystyle \int_0^1 \frac{\ln(1+y^2)}y \, dy = - \sum_(n=1)^\infty \frac{(-1)^n}n \int_0^1 y^(2n-1) \, dy = -\frac12 \sum_(n=1)^\infty ((-1)^n)/(n^2) = (\pi^2)/(24)`

`\displaystyle \int_0^1 (y \ln(y))/(1+y^2) \, dy = \sum_(n=0)^\infty (-1)^n \int_0^1 y^(2n+1) \ln(y) \, dy = -\frac14 \sum_(n=0)^\infty ((-1)^n)/((n+1)^2) = -(\pi^2)/(48)`

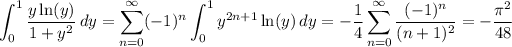
Putting everything together, we have

`\displaystyle \int_0^(\frac\pi2) \cot(x) \ln(\sec(x)) \, dx = \frac12*(\pi^2)/(24) - \left(- (\pi^2)/(48)\right) = \boxed{(\pi^2)/(24)}`