Question

Find f(-2) and g(5)
f(x)=-2x³-5 g(x)=-4x+2

Answer 1

f( -2) = 11

g(5) = - 18

Explanation:

#1. Solving for f(-2)

We're given a function "f" such that when it accepts a variable x, it's output, f(x), is:

`\boxed{ \mathsf{f(x) = - 2 {x}^(3) - 5}}`

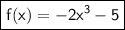
The value of f(x) depends upon what value of x is being inserted.

If x = -2

All the places taken by x will be given to -2

`\implies \mathsf{f( - 2) = - 2( { - 2}^(3) )- 5 }`

(-2)³ is the cube of (-2) with -8 as it's result

`\implies \mathsf{f( - 2) = - 2( { - 8}^{} )- 5 }`

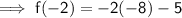
when there's no operating sign between two numbers from different origin, they're multiplied

`\implies \mathsf{f( - 2) = 16 - 5 }`

`\implies \mathsf{f( - 2) = 11 }`

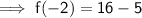
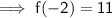
That gives us the value of f(-2) :

11

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

#2. Solving for g(5):

Here's another function, "g", taking x as input and giving us an output g(x), such that:

`\boxed{ \mathsf{g(x) = - 4x + 2}}`

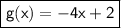
If x = 5

All the positions taken by x will be given to 5:

`\implies \mathsf{g(5) = - 4(5) + 2}`

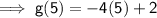
no sign between two numbers from different origin results in their product.

`\implies \mathsf{g(5) = - 20+ 2}`

`\implies \mathsf{g(5) = - 18}`

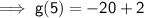
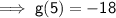
Thus, the value of g(5) is:

-18