Question

Someone help? The covered word is 'numerator'. ​

Answer 1

Hello XxItzYourLifexX!

`\huge \boxed{\mathbb{QUESTION} \downarrow}`

• Find the required fraction.

`\large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}`

Let's take the fraction as x/y , where x = numerator & y = denominator.

Given,

1st condition :-

`\rightarrow (x + 1)/(y - 1) = 1 \: \: \: \: \: \: \: \: \: - - (1) \\`

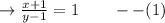
2nd condition :-

`\rightarrow (x)/(y + 1) = (1)/(2)\: \: \: \: \: \: \: \: \: - - (2) \\`

__________________

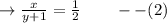
Now, let's take eq. (2) & find the value of x using cross multiplication.

`(x)/(y + 1) = (1)/(2) \\ 2x = 1(y + 1) \\ 2x = y + 1 \\ x = (y + 1)/(2)`

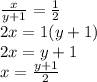
We got x as y+1/2. Now, let's substitute this value of x in eq. (1) & solve it using cross multiplication.

`(x + 1)/(y - 1) = 1 \\ ( (y + 1)/(2) + 1 )/(y - 1) = 1 \\ ( (y + 1)/(2) + 1)/(y - 1) = (1)/(1) \\ (y + 1)/(2) + 1 = y - 1 \\ (y + 3)/(2) = y - 1 \\ y + 3 = 2(y - 1) \\ y + 3 = 2y - 2 \\ y - 2y = - 2 - 3 \\ - y = - 5 \\ \boxed{ y = 5}`

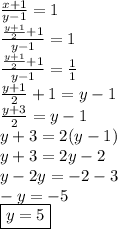
The value of y is 5. Now, let's find x. (x = y+1/2)

`x = (y + 1)/(2) \\ x = (5 + 1)/(2) \\ x = (6)/(2) \\ \boxed{x = 3}`

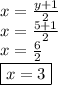
So, the values of x & y respectively are 3 & 5. Now, the required fraction will come in the form of x/y. So, the fraction is...

`(x)/(y) \\ = \large\boxed{\boxed{ \bf(3)/(5) }}`

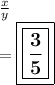
• The correct answer is 3/5 (option b).

__________________

Hope it'll help you!

ℓu¢αzz ッ