Answer: 0.063 < p < 0.137
====================================================
Step-by-step explanation:
The spreadsheet is shown below.
In cell B6, the formula used is the NORMINV function to get the z critical value. The name is the result of putting the words "NORM" and "INV" together, which refers to the inverse normal.
It's used to find the value of k in P(-k < Z < k) = 0.99, which in this case is roughly k = 2.576 so the z critical value is roughly z = 2.576
What you type in specifically is
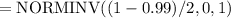
The (1-0.99)/2 portion ensures that we get the alpha/2 value which in this case is 0.005
The 0,1 at the end refers to the mean and standard deviation respectively of the standard normal Z distribution.
The output of that NORMINV function is then made positive and then you'd round to 3 decimal places.
So that's how we can get excel to display z = 2.576
----------
The margin of error E formula is
E = z*sqrt(phat*(1-phat)/n)
which doesn't need an excel function to get the job done, though of course excel can handle it just fine. You'd type in the formula as shown, but be sure to reference the correct cells.
Once E is calculated, we compute the following
which are the lower (L) and upper (U) bounds of the confidence interval.
The results are L = 0.063 and U = 0.137
That confidence interval can be written in the form (0.063, 0.137) which is equivalent to saying 0.063 < p < 0.137