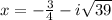Question

Someone please help me

Answer 1

Solutions:
`x = (-3)/( 4) + i √(39)`,
`x = (-3)/(4) - i √(39)`

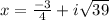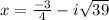
Explanation:

Given the quadratic equation, 2x² + 3x + 6 = 0, where a =2, b = 3, and c = 6:

Use the quadratic equation and substitute the values for a, b, and c to solve for the solutions:

`x = \frac{-b +/- \sqrt{b^(2) - 4ac} }{2a}`

`x = \frac{-3 +/- \sqrt{3^(2) - 4(2)(6)} }{2(2)}`

`x = (-3 +/- √(9- 48) )/(4)`

`x = (-3 +/- √(-39) )/(4)`

`x = (-3 + i √(39) )/(4)`,
`x = (-3 - i √(39) )/(4)`

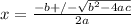
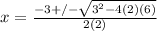
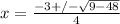
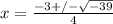
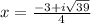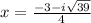
Therefore, the solutions to the given quadratic equation are:

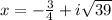`x = -(3)/( 4) + i √(39)` ,
`x = -(3)/(4) - i √(39)`