Answer:
(a)
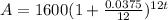
(where
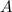 is the account balance and
is the account balance and
 is the time in years)
is the time in years)
(b) $1,929.40
Explanation:
Compound interest formula

where:
- A is the amount
- P is the principal
- r is the interest rate (in decimal form)
- t is time
- n is the number of times the interest is compounded per unit of t
Given:
- P = $1600
- r = 3.75% = 3.75/100 = 0.0375
- t = number of years
- n = 12 (as the interest is compounded monthly and t is number of years)
Substituting these values into the formula:
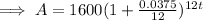
(where
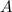 is the account balance and
is the account balance and
 is the time in years)
is the time in years)
Part (b)
Substitute
 into the equation created in part (a):
into the equation created in part (a):
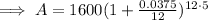
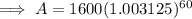
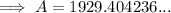
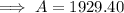
Therefore, her account balance after 5 years will be $1,929.40