Question

Please help??? i’m not sure the answers or how to do this. greatly appreciated

Answer 1

1)

I think you should start off by solving the function equal to the given growth.

`f(m) = 5.98`

`3(1.09) {}^(m) = 5.98`

`1.09 {}^(m) = (5.98)/(3)`

`1.09 {}^(m) = 1.9933`

`m * ln(1.09) = ln(1.9933)`

`m = ( ln(1.9933) )/( ln(1.09) ) = 8`

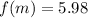
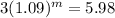
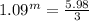
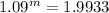
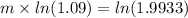
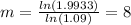
It is sufficient to plot the exponential growth over the domain m [0,8]

2)

The y-intercept in this case represents the growth achieved at the beginning when m=0.

Before the experiment started::

3)

I'm not really sure about this one,but i think it's supposed to be solved according to this eq,,

`c = (f(8) - f(2))/(8 - 2)`

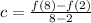
Note that c is the average rate of change.

Find f(2) first by substituting 2 in f(m)

f(2)=3(1.09)²=3.5643

`c = (5.98 - 3.5643)/( 8 - 2)`

`c = (2.4157)/(6) = 0.4026`

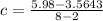
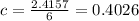
average growth=0.4026 cm/month