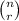Question

I want full explanation​

Answer 1

See below

Explanation:

we would like to prove the following question:

`\displaystyle \sum _(r = 0) ^(n) {3}^(r) \ \binom{n}{r} = {4}^(n)`

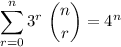
In order to do so, recall binomial theorem:

`\displaystyle \sum _(r= 0) ^(n) {a}^(n - r) {b}^(r) \ \binom{n}{r} = (a + b {)}^(n)`

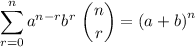
where:

• n refers to the degree of a binomial
• C(n,k) is the coefficient of the each term

Considering the given problem,if we assume a and b are 1 and 3 respectively then it can be proved easily so let's try it!

`\displaystyle \sum _(r= 0) ^(n) {1}^(n - r) {3}^(r) \ \binom{n}{r} \stackrel {?}{ = } (1 + 3 {)}^(n)`

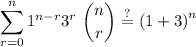
remember that,any power to 1 always yields 1 therefore we can drop
`1^(n-r)` so, we acquire:

`\displaystyle \sum _(r= 0) ^(n) {3}^(r) \ \binom{n}{r} \stackrel {?}{ = } (1 + 3 {)}^(n)`

simplify right hand side:

`\displaystyle \sum _(r= 0) ^(n) {3}^(r) \ \binom{n}{r} \stackrel { \checkmark}{ = } (4{)}^(n)`

hence we are done!

note:
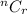`{}^n C_r` is also written as
`\binom{n}{r}`