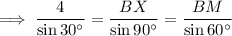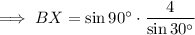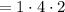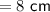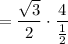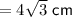Answer:
m∠X = 60°
BX = 8 cm
BM = 4√3 cm
Explanation:
The sum of the interior angles of a triangle is 180°
Given:
⇒ m∠B + m∠M + m∠X = 180°
⇒ 30° + 90° + m∠X = 180°
⇒ 120° + m∠X = 180°
⇒ m∠X = 180° - 120°
⇒ m∠X = 60°
Using the sine rule to find the side lengths:
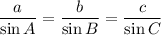
(where A, B and C are the angles, and a, b and c are the sides opposites the angles)
Given:
- m∠X = 60°
- m∠B = 30°
- m∠M = 90°
- MX = 4 cm