The writing in red is correct. The inequality sign flips when we divide both sides by a negative value.
To see why the sign flips, think of it like this:
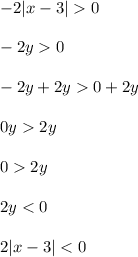
Where
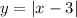 is used to condense things a bit.
is used to condense things a bit.
In short, we go from
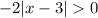 to
to
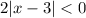 and we have a sign flip.
and we have a sign flip.
The '2' is never negative, and same goes for
 . So overall, the entire left hand side is never negative. So there are no solutions to
. So overall, the entire left hand side is never negative. So there are no solutions to
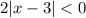 which further means there are no solutions to
which further means there are no solutions to
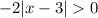
Put another way, the original inequality has its left side always as some negative number (assuming x is not equal to 3). There's no way to have a negative number larger than 0. So we have a contradiction leading to no solutions.
Answer: There are no solutions