Answer:
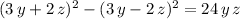
Explanation:
Make use of the fact that for any
 and
and
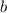 :
:
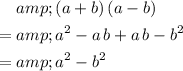 .
.
In other words, the difference
 between two squares could be written as the product of
between two squares could be written as the product of
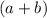 and
and
 .
.
Apply this identity to rewrite and simplify the expression in this question. In this example,
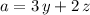 whereas
whereas
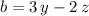 .
.
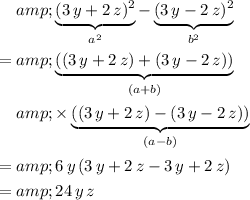 .
.