Question

Evaluate the double integral int int y^3 dA where D is the triangular region with vertices (0,1), (7,0) and (1,1).

Answer 1

1/5

Explanation:

Refer to the image for the region. I've chosen to "scan" the region horizontally for convenience sake, so x varies for values between the green and the red line, and y varies from 0 to 1.

The two lines have equations
`x=7-6y` (red line) and
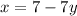`x=7-7y` (green line). Since we're integrating first with respect to x, it's easier to write the equation like that and not as
`y=mx+q` since they will become our new limits of integration

Our double integral will become

`\int \limits_0^1 \ \ \int \limits_(7-7y)^(7-6y)y^3dxdy = \int \limits_0^1 y^3x|\limits_(7-7y)^(7-6y) dy =\\\int \limits_0^1 y^3[(7-6y)-(7-7y)]dy = \int \limits_0^1y^3(y)dy =\\\int \limits_0^1 y^4dy =\frac15y^5|\limits_0^1=\frac15`