Answer:
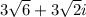 and
and
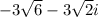
Explanation:
For a complex number
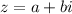 in rectangular form, polar form is
in rectangular form, polar form is
![z=r[cos(\theta)+isin(\theta)]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/4d4ht47qruebjyfcx7pu.png) where
where
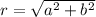 and
and
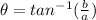 :
:
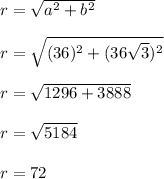
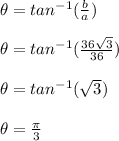
Thus, our complex number in polar form is
![z=72[cos((\pi)/(3))+isin((\pi)/(3))]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/i319u9fuwpcemg3xvl76.png) . This will help us determine the square roots of the complex number using the formula
. This will help us determine the square roots of the complex number using the formula
![\sqrt[n]{r}\biggr[cis\bigr({(\theta+2\pi k)/(n))\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/k5kh6myoj3zc0zruibk5.png) for
for
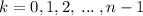 . Note that
. Note that
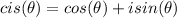 :
:
1st square root for k = 2-1 = 1
![\sqrt[n]{r}\biggr[cis\bigr({(\theta+2\pi k)/(n))\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/k5kh6myoj3zc0zruibk5.png)
![\sqrt[2]{72}\biggr[cis\bigr({((\pi)/(3)+2\pi(1))/(2))\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5vg5nz8fbjy0f3udwaco.png)
![6√(2)\biggr[cis\bigr({((\pi)/(3)+2\pi)/(2))\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/wko7t5sox85wlngw5qlz.png)
![6√(2)\biggr[cis\bigr((\pi)/(6)+\pi)\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/9vuvh7g68e8ler0cpbo5.png)
![6√(2)\biggr[cis\bigr((7\pi)/(6))\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/t3djkj7f26lu1t7zatmf.png)
![6√(2)\biggr[cos((7\pi)/(6))+isin((7\pi)/(6))\biggr]\\ \\6√(2)(-(√(3))/(2)-(1)/(2)i)\\\\-3√(6)-3√(2)i](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/68au9w0ui5naeme1u121.png)
2nd square root for k = 1-1 = 0
![\sqrt[6]{72}\biggr[cis\bigr({((\pi)/(3)+2\pi(0))/(2)\bigr)\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/u1wmllz1nebbbjkrzxb6.png)
![6√(2)\biggr[cis((\pi)/(6) )\biggr]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/kv1b79w33q3ioym893gc.png)
![6√(2)[cos((\pi)/(6))+isin((\pi)/(6))]\\ \\6√(2)((√(3))/(2)+(1)/(2))\\\\3√(6)+3√(2)i](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/fqgoxdq8oph3mgccvmh8.png)
Therefore, the square roots of
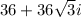 are
are
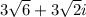 and
and
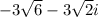 .
.