1 Answer

Ember Arlynx · Answer 1 · 2022-07-23T11:35:49+0000

$\large\underline{\sf{Solution-}}$

We have to find out the value of the fraction.

Let us assume that:

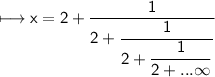
$\sf \longmapsto x =2 + (1)/(2 + (1)/(2 + (1)/(2 + ... \infty) ) )$

We can also write it as:

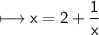
$\sf \longmapsto x =2 + (1)/(x)$

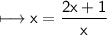
$\sf \longmapsto x =(2x + 1)/(x)$

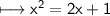
$\sf \longmapsto {x}^(2) =2x + 1$

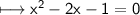
$\sf \longmapsto {x}^(2) - 2x - 1 = 0$

Comparing the given equation with ax² + bx + c = 0, we get:

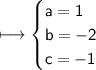
$\sf \longmapsto\begin{cases} \sf a =1 \\ \sf b = - 2 \\ \sf c = - 1 \end{cases}$

By quadratic formula:

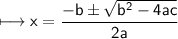
$\sf \longmapsto x = \frac{ - b \pm \sqrt{ {b}^(2) - 4ac } }{2a}$

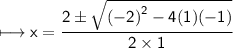
$\sf \longmapsto x = \frac{2 \pm \sqrt{ {( - 2)}^(2) - 4(1)( - 1)} }{2 * 1}$

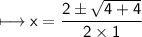
$\sf \longmapsto x = (2 \pm √(4 + 4) )/(2 * 1)$

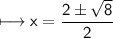
$\sf \longmapsto x = (2 \pm √(8) )/(2)$

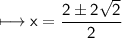
$\sf \longmapsto x = (2 \pm2 √(2) )/(2)$

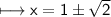
$\sf \longmapsto x = 1 \pm√(2)$

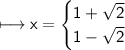
$\sf \longmapsto x = \begin{cases} \sf 1 + √(2) \\ \sf 1 - √(2) \end{cases}$

But "x" cannot be negative. Therefore:

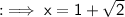
$\sf :\implies x = 1 + √(2)$

So, the value of the fraction is 1 + √2.

Please log in or register to add a comment.