Question

`\rm\frac{13}8 + \sum \limits_(n = 0)^( \infty ) \frac{( - {1)}^(n + 1) (2n + 1)! }{n! (n + 2)! {4}^(2n + 3) } \\`​

Answer 1

Rewrite the factorial parts of the summand as

`((2n+1)!)/(n!(n+2)!) = ((2n+1)(2n!))/((n+2)(n+1)(n!)^2) = (2n+1)/((n+2)(n+1)) \dbinom{2n}n`

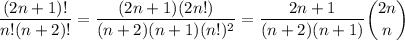
where
`\binom nk` is the binomial coefficient, and
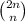`\binom{2n}n` are the so-called central binomial coefficients.

Expand the rational expression into partial fractions:

`(2n+1)/((n+2)(n+1)) = \frac3{n+2} - \frac1{n+1}`

Pull out a constant factor and collect the exponential terms.

`((-1)^(n+1))/(4^(2n+3)) = -\frac1{64} \left(-\frac1{16}\right)^n`

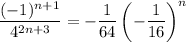
The sum we want is now

`\displaystyle \frac{13}8 - \frac1{64} \sum_(n=0)^\infty \binom{2n}n \left(\frac3{n+2} - \frac1{n+1}\right) \left(-\frac1{16}\right)^n`

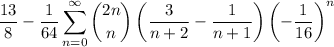
Let f(x) and g(x) be functions with power series expansions

`\displaystyle f(x) = \sum_(n=0)^\infty \binom{2n}n (x^n)/(n+1)`

`\displaystyle g(x) = \sum_(n=0)^\infty \binom{2n}n (x^n)/(n+2)`

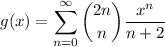
and recall the well-known binomial series

`\displaystyle \frac1{√(1-4x)} = \sum_(n=0)^\infty \binom{2n}n x^n`

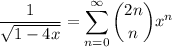
which converges for |x| < 1/4.

Integrating both sides yields

`\displaystyle \int (dx)/(√(1-4x)) = \int \sum_(n=0)^\infty \binom{2n}n x^n \, dx`

`\displaystyle -\frac12 √(1-4x) = C_1 + \sum_(n=0)^\infty \binom{2n}n (x^(n+1))/(n+1)`

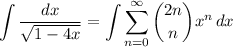
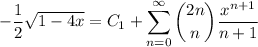
Taking x = 0 on both sides, it follows that C₁ = -1/2. We then see that

`\displaystyle f(x) = (1-√(1-4x))/(2x)`

Step back and multiply both sides of the binomial series identity by x, then integrate. This yields

`\displaystyle \int \frac x{√(1-4x)} \, dx = \int \sum_(n=0)^\infty \binom{2n}n x^(n+1) \, dx`

`\displaystyle -\frac1{12} √(1-4x) (1 + 2x) = C_2 + C_1 x + \sum_(n=0)^\infty \binom{2n}n (x^(n+2))/(n+2)`

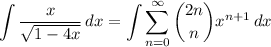
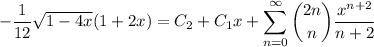
Taking x = 0 again points to C₂ = -1/12. Hence

`\displaystyle g(x) = (1 - √(1-4x)(1+2x))/(12x^2)`

Then the value of the sum we want is

`\displaystyle \frac{13}8 - \frac1{64} \left(3g\left(-\frac1{16}\right) - f\left(\frac1{16}\right)\right) = \frac{1+\sqrt5}2 = \boxed{\phi}`

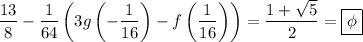
where ɸ ≈ 1.618 is the golden ratio.