Answers:

and
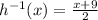
See note below
====================================================
Step-by-step explanation:
First we replace f(x) with y. Then we swap x and y. Afterward, solve for y to determine the inverse function. The m value cannot be zero to avoid dividing by zero.

-----------------
For the formula h(x) = 2x-9, we see that m = 2 and b = -9
So the inverse for h(x) would be:
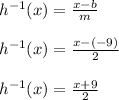
-----------------
Note: The function
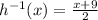 is the same as saying
is the same as saying
 or
or
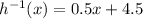 , so it will depend on what format your teacher wants.
, so it will depend on what format your teacher wants.