Question

Please help!

A restaurant sells tea for

$1.50 per drink. The cost of drinks, F(d), can be found by using the function F(d) = 1.5d. If the restaurant sells no more

than $150 in drinks in a day, what is a reasonable domain and range


Thank you!


Domain:



Range:

Answer 1

Answers:

Domain is
`0 \le d \le 100`

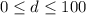
Range is
`0 \le F(d) \le 150`

==============================================

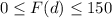
Step-by-step explanation:

The most money made from selling drinks is $150. Divide this over the cost per drink to get 150/(1.50) = 100; indicating that at most 100 drinks are sold per day. This is the largest that d can get because d represents the number of drinks sold.

The smallest d can get is d = 0 to mean that no drinks are sold.

In short: d is between 0 and 100, including both endpoints. We write
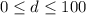`0 \le d \le 100` to indicate this. This is the domain because the domain represents all the possible inputs allowed.

---------------------------------------------------

The range is the set of allowed outputs.

If we plugged in d = 0, then you would find F(d) = 0 as well. If you don't sell any drinks, then you earn $0. This is the smallest item in the range.

On the other side of things, the largest item in the range is 150 because this value was given to us. It's the upper limit or ceiling value of how much money is made from drinks. You can also find this by plugging d = 100, the largest domain value, into the function to get F(d) = 150.

Therefore the range is
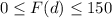`0 \le F(d) \le 150` to indicate that F(d) is between 0 and 150 inclusive of both endpoints.