Question

I’m so lost i have no idea how to get the function please see pic

Answer 1

You should first recognize the shape of the curve - it's an exponential function, so its equation takes the form
`y(x)=a\cdot b^(cx)` for some constants a, b, and c.

The curve lies above the x-axis, so a must be positive.

The curve is defined everywhere (there are no discontinuities), so b must be positive.

As you move left to right, the function is increasing, so c must also be positive. But to make things simpler, let's assume c = 1.

When x = 0, the curve passes through the point (0, 1). In our equation, we have

`y(0) = a\cdot b^0 = a`

so it follows that a = 1.

When x = 1, the curve approximately passes through the point (1, 4); so

`y(1) = b^1 = 4`

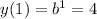
so b = 4.

Then the equation of the curve might be
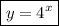`\boxed{y = 4^x}`.