The final velocity (
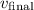 ) is positive, indicating that the car continues to move in the same direction after the collision. Therefore, option A is the correct prediction.
) is positive, indicating that the car continues to move in the same direction after the collision. Therefore, option A is the correct prediction.
To determine the motion of the toy car immediately after the collision, we can apply the principles of linear momentum. The conservation of linear momentum states that the total linear momentum of an isolated system remains constant if no external forces act on it.
The initial linear momentum (
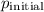 ) of the system is given by the mass of the car (m) multiplied by its initial velocity (
) of the system is given by the mass of the car (m) multiplied by its initial velocity (
 ):
):
![\[ p_{\text{initial}} = m \cdot v_{\text{initial}} \]](https://img.qammunity.org/2023/formulas/physics/high-school/3f78lrbsji4j229b3ehs7rchkiyueoccv2.png)
The final linear momentum (
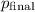 ) of the system is given by the mass of the car multiplied by its final velocity (
) of the system is given by the mass of the car multiplied by its final velocity (
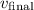 ):
):
![\[ p_{\text{final}} = m \cdot v_{\text{final}} \]](https://img.qammunity.org/2023/formulas/physics/high-school/fezwg73qaeda5d6zoozwioitk0wtrnwshr.png)
Since no external horizontal forces act on the system, the horizontal component of linear momentum is conserved. Mathematically, this can be expressed as:
![\[ p_{\text{initial, horizontal}} = p_{\text{final, horizontal}} \]](https://img.qammunity.org/2023/formulas/physics/high-school/ze0pej7m1wrpu9y3ft7u1y7yp0vy1mvcap.png)
Now, let's break down the velocities into components. The initial velocity (
 ) is positive since the car is moving to the right. After the collision, the final velocity (
) is positive since the car is moving to the right. After the collision, the final velocity (
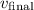 ) will have both magnitude and direction.
) will have both magnitude and direction.
Given that a force is applied in the opposite direction, we can use the impulse-momentum theorem:
![\[ \text{Impulse} = F \cdot \Delta t \]](https://img.qammunity.org/2023/formulas/physics/high-school/il6vuyh5ag0su67b588psqc0nx3rdn4uf2.png)
The change in momentum (
 ) is equal to the impulse:
) is equal to the impulse:
![\[ \Delta p = F \cdot \Delta t \]](https://img.qammunity.org/2023/formulas/physics/high-school/jsjsatc75rfhds4vyar9n64oro2zwvh2d1.png)
Now, the final velocity (
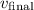 ) can be calculated using the formula:
) can be calculated using the formula:
![\[ v_{\text{final}} = v_{\text{initial}} + (\Delta p)/(m) \]](https://img.qammunity.org/2023/formulas/physics/high-school/oboy2vg28iiikzj09egb16y0nx2ks71o85.png)
Substituting the values:
![\[ v_{\text{final}} = 1.0 \, \text{m/s} + \frac{(20 \, \text{N} \cdot 0.2 \, \text{s})}{2 \, \text{kg}} \]](https://img.qammunity.org/2023/formulas/physics/high-school/gcsbytdot3tp0ijw88dn80xtxd6r9u7pst.png)
![\[ v_{\text{final}} = 1.0 \, \text{m/s} + 2.0 \, \text{m/s} = 3.0 \, \text{m/s} \]](https://img.qammunity.org/2023/formulas/physics/high-school/vtm271gy4j3nr8sl15b4qog60iz5ry090n.png)
The final velocity (
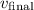 ) is positive, indicating that the car continues to move in the same direction after the collision. Therefore, option A is the correct prediction:
) is positive, indicating that the car continues to move in the same direction after the collision. Therefore, option A is the correct prediction:
A: The speed of the car will increase, and the car will travel in the opposite direction.