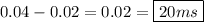Hi there!
Recall the equation for the voltage of a discharging capacitor:
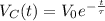
V₀ = Initial voltage of the capacitor (V)
t = Time (s)
τ or RC = Time Constant (s)
With the given information, we can plug in the value for V₀:
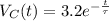
We are given that at t = 20 ms (0.02 s), the voltage of the capacitor is 0.8V. We can use this to solve for the time constant (τ).
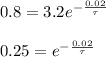
Take the natural log of both sides and solve.
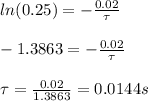
Now, we can use this time constant to solve for the time taken for the voltage to drop from 0.8 V to 0.2 V. Solve for the time taken for the capacitor's voltage to drop to 0.2 V:
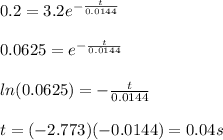
Now, subtract the times: