Answer:
D
Explanation:
When a polynomial f(x) is divided by (x - a) then remainder is f(a)
A
divided by (x + 4 ), then a = - 4
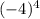 - 8(- 4)² + 16 = 256 - 128 + 16 = 144 ≠ 20
- 8(- 4)² + 16 = 256 - 128 + 16 = 144 ≠ 20
B
divided by (x - 2), then a = 2
3(2)³ + 7(2)² + 5(2) + 2
= 3(8) + 7(4) + 10 + 2
= 24 + 28 + 12 = = 64 ≠ 20
C
divided by (x + 5) , then a = - 5
(- 5)³ + 5(- 5)² - 4(- 5) + 6
= - 125 + 125 + 20 + 6 = 26 ≠ 20
D
divided by (x - 2), then a = 2
3
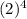 - 5(2)³ + 5(2) + 2
- 5(2)³ + 5(2) + 2
= 3(16) - 5(8) + 10 + 2
= 48 - 40 + 12 = 20 ← Remainder of 20