Answer:
10:A 11:D
Explanation:
10)
g(

rewrite
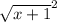 as x +1
as x +1
g
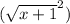 =
=
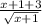
add 1+3
g
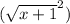 =
=
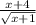
combine and symplify
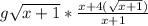
reorder factors of the second side
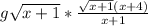
take out the root x+1
and you are left with A
11.
f(g(x))
substitue g into f
f(
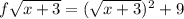
rewrite sqrroot x+3 as x+3
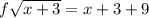
Now add 3+9
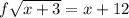
we get x+12
Now for domain
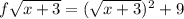
set the radicand root sqr x+3 >= 0 to find the expression defined
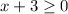
subtract 3 from both sides
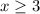
turn it into interval notation
[-3,+∞)