Question

What is the remainder when 2^81 is divided by 17? Need 3 answer with solution! ​

Answer 1

Answer: 2

==========================================================

Step-by-step explanation:

Note that 2^4 = 16 is one less than 17.

Because of this nature of being 1 less, we can say the remainder of 16/17 is -1 because it comes up one short.

In terms of modular arithmetic, we can say,

`2^4 \equiv 16 \ (\text{mod } 17)\\\\2^4 \ \equiv -1 (\text{mod } 17)\\\\`

Then let's raise both sides to the 20th power. I'm picking 20 because 20*4 = 80 which will help build toward 81

`2^4 \equiv -1 \ (\text{mod } 17)\\\\\left(2^4\right)^(20) \equiv (-1)^(20) \ (\text{mod } 17)\\\\2^(20*4) \equiv 1 \ (\text{mod } 17)\\\\2^(80) \equiv 1 \ (\text{mod } 17)\\\\`

Lastly, we'll multiply both sides by 2 to get to the final answer

`2^(80) \equiv 1 \ (\text{mod } 17)\\\\2*2^(80) \equiv 2*1 \ (\text{mod } 17)\\\\2^(1)*2^(80) \equiv 2 \ (\text{mod } 17)\\\\2^(1+80) \equiv 2 \ (\text{mod } 17)\\\\2^(81) \equiv 2 \ (\text{mod } 17)\\\\`

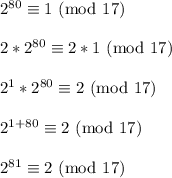
So if we were to divide 2^81 over 17, then we get some quotient and a remainder of 2