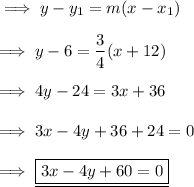Question

Write an equation in slope-intercept form

of the line that passes through the point
(-12,6) and is perpendicular to the line
X= - 3/4y -5 ( What would be my first step to put that equation into slope intercept form?) 

Answer 1

Hint :-

• The product of slopes of two perpendicular lines is -1 .
• The slope intercept form of the line is
  `y = mx + c` .
• The point slope form of the line is
  `m(x-x_1) = (y-y_1)`

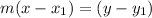
Solution :-

The given equation to us is ,

`\implies x = (-3)/(4)y - 5`

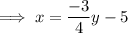
Convert it to slope intercept form we have ,

`\implies 4x =-3y -20 \\\\\implies 3y = -4x -20 \\\\\implies y =(-4)/(3)x -(20)/(3)`

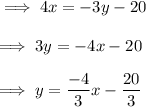
On comparing to the slope intercept form of the line we have ,

• 
  `m = (-4)/(3)`

As we know that the product of slopes of two perpendicular lines is-1 , henceforth ,

• 
  `m_(perp)= (3)/(4)`

Now using slope point form rewrite the equation of the perpendicular line ,

`\implies y-y_1 = m(x-x_1) \\\\\implies y -6 = (3)/(4)(x+12)\\\\\implies 4y -24 = 3x + 36 \\\\\implies 3x -4y +36+24=0\\\\\implies \underline{\boxed{ \gray{3x -4y +60=0}}}`