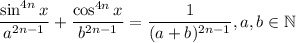Answer:
See below
Explanation:
Considering
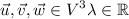 , then
, then
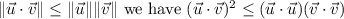
This is the Cauchy–Schwarz Inequality, therefore
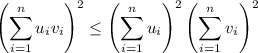
We have the equation
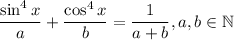
We can use the Cauchy–Schwarz Inequality because
 and
and
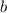 are greater than 0. In fact,
are greater than 0. In fact,
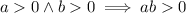 . Using the Cauchy–Schwarz Inequality, we have
. Using the Cauchy–Schwarz Inequality, we have
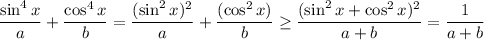
and the equation holds for
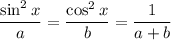
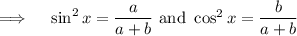
Therefore, once we can write
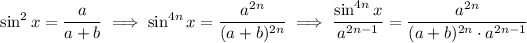
It is the same thing for cosine, thus
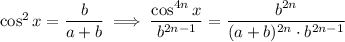
Once
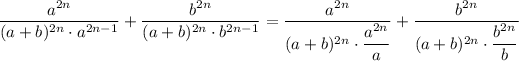
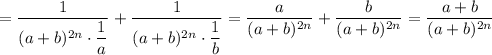
dividing both numerator and denominator by
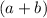 , we get
, we get
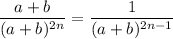
Therefore, it is proved that