Explanation:
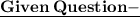
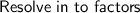
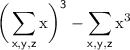

Given expression is
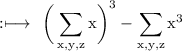
can be rewritten as
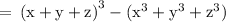
can be further rewritten as
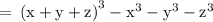
![\rm \: = \: [{(x + y + z)}^(3) - {x}^(3)] - [{y}^(3) + {z}^(3)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/6ru6jmh50osbr6t0iu8plvj1l9xq0tu6qg.png)
We know,
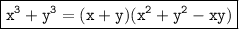
and
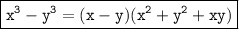
So, using these Identities, we get
![\rm =(x + y + z - x)[ {(x + y + z)}^(2) + {x}^(2) - x(x + y + z)] - (y + z)( {y}^(2) + {z}^(2) - yz)](https://img.qammunity.org/2022/formulas/mathematics/high-school/1uij8ycgbjh67yi4wcl47d0jt3ta05h0ce.png)
![\rm =(y + z)[ {(x + y + z)}^(2) + {x}^(2) + {x}^(2) + xy + xz] - (y + z)( {y}^(2) + {z}^(2) - yz)](https://img.qammunity.org/2022/formulas/mathematics/high-school/7jszzzkb8djdwl5llkibktzp1o5o9x02z6.png)
![\rm =(y + z)[ {(x + y + z)}^(2) + {2x}^(2) + xy + xz] - (y + z)( {y}^(2) + {z}^(2) - yz)](https://img.qammunity.org/2022/formulas/mathematics/high-school/7wu17eiedtz7yv7p3xunyz3s125gn4vbjx.png)
![\rm =(y + z)[ {(x + y + z)}^(2) + {2x}^(2) + xy + xz - {y}^(2) - {z}^(2) + yz]](https://img.qammunity.org/2022/formulas/mathematics/high-school/a7t9t0zrhas45waezjqmwseb8uxhrf4lbd.png)
![\rm =(y + z)[ {x}^(2)+{y}^(2)+{z}^(2) + 2xy + 2yz + 2zx + {2x}^(2) + xy + xz - {y}^(2) - {z}^(2) + yz]](https://img.qammunity.org/2022/formulas/mathematics/high-school/80zvhi92jpy3u6k80dpwhgot1phcgqjn74.png)
![\rm =(y + z)[3{x}^(2) + 3xy + 3yz + 3zx]](https://img.qammunity.org/2022/formulas/mathematics/high-school/56o799mo8grwtlk4779asrdrncij0bdcyw.png)
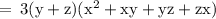
![\rm \: = \: 3(y + z)[x(x + y) + z(x + y)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/mp4tdkw9a7jannj8xs5oo2gjjuo5s4kco5.png)
![\rm \: = \: 3(y + z)[(x + y)(x + z)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/xwo8dz690uvuw2a8ziclepvacbxyggc919.png)
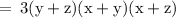
Hence,
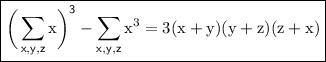
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
More Identities to know:-
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
a² - b² = (a + b)(a - b)
(a + b)² = (a - b)² + 4ab
(a - b)² = (a + b)² - 4ab
(a + b)² + (a - b)² = 2(a² + b²)
(a + b)³ = a³ + b³ + 3ab(a + b)
(a - b)³ = a³ - b³ - 3ab(a - b)