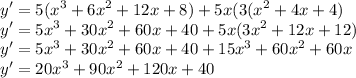Answer:
(i)

(ii/(a))
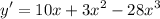
(ii/(b))

Explanation:
( 1 )
For first question, we have to use first principal or limit definition to find the derivative of 3x^2-2x.
Limit Definition of Derivative
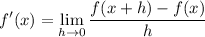
Our f(x) is 3x^2-2x.
Our f(x+h) is 3(x+h)^2-2(x-h)
![\displaystyle \large{f'(x) = \lim_(h \to 0) \frac{[3 {(x + h)}^(2) - 2(x + h)]- (3 {x}^(2) - 2x) }{h} }](https://img.qammunity.org/2022/formulas/mathematics/high-school/wi8sfmqaekswo0w9e9qqxx3euwkeeuyyuv.png)
Expand the expressions and simplify:-
![\displaystyle \large{f'(x) = \lim_(h \to 0) \frac{[3 ( {x}^(2) + 2xh + {h}^(2)) - 2x - 2h]- 3 {x}^(2) + 2x}{h} } \\ \displaystyle \large{f'(x) = \lim_(h \to 0) \frac{3 {x}^(2) + 6xh + 3{h}^(2) - 2x - 2h - 3 {x}^(2) + 2x}{h} } \\ \displaystyle \large{f'(x) = \lim_(h \to 0) \frac{6xh + 3 {h} ^(2) - 2h}{h} }](https://img.qammunity.org/2022/formulas/mathematics/high-school/16tk3uxoliru3c96hxyope7oxx6aw48llx.png)
Cancel all h's.

Substitute h = 0
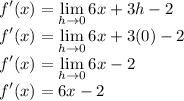
Therefore, the derivative of 3x^2-2x is 6x-2 by first principal.
( 2 )
For the second question, there are two sub-questions. Assume that you can use any formulas to differentiate instead of using first principal.
(a)
We are given the function:
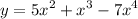
Our formula for derivative of polynomial function is:-
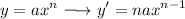
Apply the formula:-
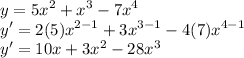
If you want it in factored form then:-
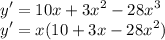
Alternative
You can factor the expression then apply product rules.
Product Rules
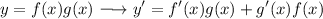
Therefore:-
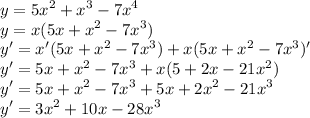
( b )
For our second sub-question, you can apply product rules instead of expanding in and differentiate.
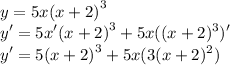
Recall cubic formula:
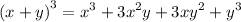
Therefore:-