Answer:
Scale factor:
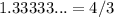
Actual area:

Scale drawing area:
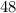
Ratio of areas:
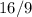
Scale factor 2:

Scale factor
 :
:

Scale factor
 :
:
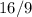
Observation: The ratio of the areas of the triangles is the square of the scale factor of the sides
Scale factor
 :
:
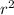
Explanation:
The scale factor is
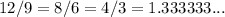
The actual area is
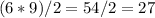
The scale drawing area is
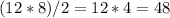
Ratio of areas:
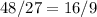
When the scale factor of the sides was 2, then the value of the ratio of the areas was 4.
When the scale factor of the sides was
 , then the value of the ratio of the areas was
, then the value of the ratio of the areas was
 .
.
When the scale factor of the sides was
 , then the value of the ratio of the areas was
, then the value of the ratio of the areas was
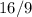 .
.
Observation: The ratio of the areas of the triangles is the square of the scale factor of the sides.
If the scale factor is
 , then the ratio of the areas is
, then the ratio of the areas is
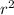 , based on the observation.
, based on the observation.
Extra: Proof of observation.
Let the legs of the actual triangle be
 and
and
 . Then the legs of the scale triangle are
. Then the legs of the scale triangle are
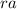 and
and
 , with
, with
 being the scale factor.
being the scale factor.
The area of the actual triangle is
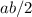 . The area of the scale triangle is
. The area of the scale triangle is
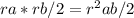 .
.
The ratio of these areas is
 , as desired.
, as desired.