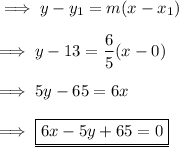Question

Street L is perpendicular to and has the same y-intercept

as the line 5x+6y= 78. Write this street's equation in
standard form.

Answer 1

`6x-5y+65=0`

Explanation:

Given equation of line ,

`\implies 5x + 6y = 78`

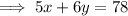
Convert it to Slope Intercept Form which is
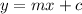`y=mx + c` , we have ,

`\implies 6y = 78 - 5x \\\\\implies y= (-5)/(6)x + 13`

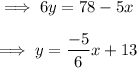
Therefore

• 
  `m =(-5)/(6)`
• 
  `c = 13`

As we know that the product of slopes of two perpendicular lines is -1 . Hence the slope of the perpendicular line will be ,

• 
  `m_(perp)= (6)/(5)`
• 
  `y- intercept = (0,13)`

On using point slope form of the line , we have ,

`\implies y - y_1 = m(x - x_1) \\\\\implies y - 13 = (6)/(5)( x - 0 ) \\\\\implies 5y - 65 = 6x \\\\\implies \underline{ \boxed{ 6x - 5y + 65 = 0 }}`