Question

Find h'(-4) if
`h=(f\circ g),` , f(x) = −6x² + 7 and the equation of the tangent line of g at -4 is y = 10x - 8

Answer 1

`h'(-4) = 5760`

Explanation:

We are given the function:

`\displaystyle h(x) = (f\circ g)(x)`

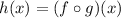
And we want to find h'(-4) given:

`\displaystyle f(x) = -6x^2 + 7`

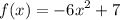
And that the equation of the tangent line of g at x = -4 is y = 10x - 8.

Recall that (f ∘ g)(x) = f(g(x)). Hence:

`\displaystyle h(x) = f(g(x))`

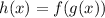
Find h'(x). We can take the derivative of both sides with respect to x:

`\displaystyle (d)/(dx)\left[ h(x)\right] = (d)/(dx)\left[ f(g(x))\right]`

By the chain rule:

`\displaystyle h'(x) = f'(g(x)) \cdot g'(x)`

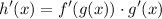
Therefore:

`\displaystyle h'(-4) = f'(g(-4)) \cdot g'(-4)`

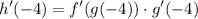
A) Finding f'(g(-4)):

Recall that we are given that the equation of the tangent line of g at x = -4 is:

`\displaystyle y = 10x - 8`

Since this is tangent, it tells us that at x = -4, line y touches g. Therefore, y(-4) = g(-4). Find y(-4):

`\displaystyle \begin{aligned} y(-4)&= 10(-4) - 8 \\ \\ &= -48\end{aligned}`

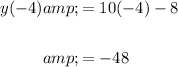
Hence, g(-4) = -48. Consequently, f'(g(-4)) = f'(-48).

Find f'(x):

`\displaystyle \begin{aligned} f'(x) &= (d)/(dx)\left[ -6x^2 + 7\right] \\ \\ &= -12x\end{aligned}`

So:

`\displaystyle \begin{aligned} f'(-48) &= -12(-48) \\ \\ &= 576\end{aligned}`

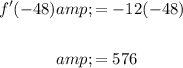
Therefore, f'(g(-4)) = 576.

B) Finding g'(-4):

Recall that by definition, the derivative of a function at a point is the slope of the tangent line to the point.

The tangent line to g at x = -4 is given by:

`y = 10 x- 8`

The slope of the line is 10. Therefore:

`g'(-4) = 10`

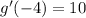
Hence:

`\displaystyle \begin{aligned}h'(-4) &= f'(g(-4)) \cdot g'(-4) \\ \\ &= (576) \cdot (10) \\ \\ &= 5760 \end{aligned}`

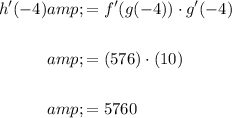
In conclusion:

`h'(-4) = 5760`