Answer:
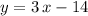 .
.
Explanation:
The slope-intercept form equation of a slanting line is in the form
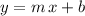 , where
, where
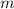 would be the slope of that line.
would be the slope of that line.
The equation of the original line is given in the slope-intercept form:
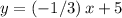 . The slope of that line would thus be
. The slope of that line would thus be
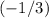 .
.
Two slanted lines in a plane are perpendicular to one another if and only if their slopes are inverse reciprocals.
In other words, if the slope of two slanted lines are
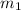 and
and
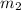 , those two lines would be perpendicular to one another if and only if
, those two lines would be perpendicular to one another if and only if
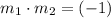 .
.
In this question, the slope of the given line is
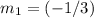 . Rearrange the equation
. Rearrange the equation
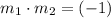 to find
to find
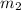 , the slope of the line perpendicular to the given line:
, the slope of the line perpendicular to the given line:
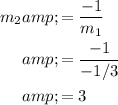 .
.
In other words, the slope of the line perpendicular to the given line would be
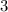 .
.
If a line of slope
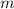 goes through the point
goes through the point
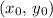 , the point-slope equation of that line would be
, the point-slope equation of that line would be
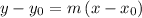 .
.
In this question, the requested line goes through the point
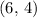 . It was also deduced that the slope of this requested line is be
. It was also deduced that the slope of this requested line is be
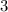 . The equation of this line in point-intercept form would be:
. The equation of this line in point-intercept form would be:
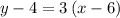 .
.
Rearrange to find the equation of this line in slope-intercept form:
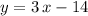 .
.