Question

Which of the following numbers can be expressed as repeating decimals?

3/7, 2/5, 3/4, 2/9

Answer 1

Part I: Defining "Repeating decimals"

Repeating decimals refers to a specific number being repeated after the decimal point in a decimal. Repeating decimals never terminates.

A few examples of repeating decimals can be 8.8888... or 8.818181...

Part II: Verifying all options and choosing the correct choice

Now, let's convert the fractions into decimals using a calculator:

• A) 3/7 ⇔ 0.428571428571...

• B) 2/5 ⇔ 0.4

• C) 3/4 ⇔ 0.75

• D) 2/9 ⇔ 0.22222222222...

Option A

This option is classified as a repeating decimal because there is specific number being repeated after the decimal point in 3/7 (428571).

To avoid confusion, we can split the decimal shown below.

⇒ A) 3/7 ⇒
`0.428571428571...` ⇒
`0.\underline{428571} \ \underline{428571}...`

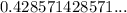It also has the three dots, which indicates that the number does not terminate. Therefore, 3/7 a repeating decimal.

Option B

This option is a terminating decimal. Terminating decimals are not allowed in repeating decimals. Therefore, 2/5 is not a repeating decimal

Option C

This option is a terminating decimal. Terminating decimals are not allowed in repeating decimals. Therefore, 3/4 is not a repeating decimal.

Option D

We can see that 2/9 has a specific number being repeated after the decimal point, which is 2. It also has the three dots, which indicates that the number does not terminate. Therefore, 2/9 is a repeating decimal