Answer:
1978 ft (nearest foot)
Explanation:
Using the Alternate Interior Angles theorem, we can deduce that the left base angle of the triangle is 32° and the right base angle of the triangle is 23°.
The triangle can be divided into 2 right triangles, both with height of 500ft (see attached diagram).
Using the tan trig ratio, we can calculate the base of each triangle.
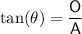
where:
 = angle
= angle- O = side opposite the angle
- A = side adjacent the angle
Left triangle
let
 = the base length
= the base length

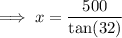
Right triangle
let
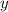 = the base length
= the base length
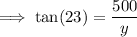

To find the distance between the Soldier Field and Adler Planetarium, simply sum
 and
and
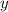 :
:
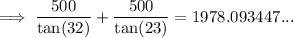
Therefore, the distance is 1978 ft (nearest foot)