Question

Hello help me with this question thanks in advance​

Answer 1

`\bold{\huge{\underline{ Solution \:1 }}}`

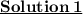
Figure 1 :-

Here, we

• One triangle and AB acts as a bisector for RT and ST.
• The length of AT and AR are 15 and 5
• The length of BT and BS are 12 and 4

By using basic proportionality theorem :-

• This theorem states that if a line which is parallel to the side of triangle intersect other to sides then the line which divides the other two sides are in proportion that means the ratios are equal

That is,

`\sf{( AT)/(RT )}{\sf{=}}{\sf{(BT)/(ST)}}`

Subsitute the required values,

`\sf{( 8 )/( 8 + 11 )}{\sf{=}}{\sf{(7)/(7 +10)}}`

`\sf{( 8 )/( 19)}{\sf{=}}{\sf{(7)/(17)}}`

`\sf{( 8 )/( 19)}{\sf{≠}}{\sf{(7)/(17)}}`

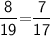
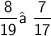
Hence, AB is not parallel to RS

Figure 2 :-

Here, we have

• One triangle and AB acts as a bisector for RT and ST.
• The length of AT and AR are 8 and 11
• The length of BT and BS are 7 and 10

By using basic proportionality theorem :-

That is,

`\sf{( AT)/(RT )}{\sf{=}}{\sf{(BT)/(ST)}}`

Subsitute the required values,

`\sf{( 15 )/( 15 + 5 )}{\sf{=}}{\sf{(12)/(16)}}`

`\sf{(15 )/( 20)}{\sf{=}}{\sf{(12)/(16)}}`

`\sf{( 3)/( 4)}{\sf{=}}{\sf{(3)/(4)}}`

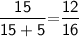
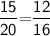
Hence, AB is parallel to RS

`\bold{\huge{\underline{ Solution\: 2}}}`

Here, we have

• Triangle ABC and DE || BC
• The length of AB = 12 , AD = 4 , DE = 6 and AC = 24 .

Part 3 :-

By using basic proportionality theorem,

• This theorem states that if a line which is parallel to the side of triangle intersect other to sides then the line which divides the other two sides are in proportion that means the ratios are equal

That is,

`\sf{( AD)/(AB )}{\sf{=}}{\sf{(AE)/(AC)}}`

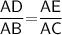
Subsitute the required values,

`\sf{( 4)/(12 )}{\sf{=}}{\sf{(AE)/(24)}}`

`\sf{( 4)/(12 )}{\sf{{*} 24= AE}}`

`\sf{ AE = 4 {*} 2 }`

`\sf{ AE = 8 }`

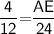
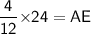
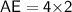
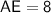
Hence, The length of AE is 8

Part 4 :-

Again , By using Basic proportionality theorem :-

That is

`\sf{( AD)/(AB )}{\sf{=}}{\sf{(DE)/(BC)}}`

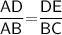
Subsitute the required values,

`\sf{( 4)/(12 )}{\sf{=}}{\sf{(6)/(BC)}}`

`\sf{( 1)/(3 )}{\sf{=}}{\sf{(6)/(BC)}}`

`\sf{ BC = 6 {*} 3 }`

`\sf{ BC = 18 }`

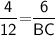
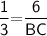
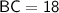
Hence, The length of BC is 18 .