Question

Can someone help me please?

Answer 1

Length of the diameter of the circle = 10 units long

Explanation:

Given points A (0, -7) and B (8, -1):

We can determine the diameter of the circle by solving for the distance between the two given points.

We'll use the following distance formula:

`d = \sqrt{(x_(2) - x_(1))^(2) + (y_(2) - y_(1))^(2) }`

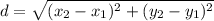
Let
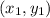`(x_(1), y_(1))` = (0, -7)

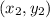`(x_(2), y_(2))` = (8, -1)

Plug in these values into the distance formula

`d = \sqrt{(x_(2) - x_(1))^(2) + (y_(2) - y_(1))^(2) }`

`d = \sqrt{(8 - 0)^(2) + (-1 - (-7))^(2) }`

`d = \sqrt{(8)^(2) + (-1 + 7)^(2) }`

`d = \sqrt{(8)^(2) + (6)^(2) }`

`d = √(64 + 36)`

`d = √(100)`

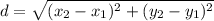
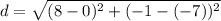
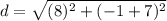
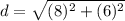
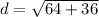
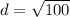
d = 10

Therefore, the distance between points A and B is 10 units long.