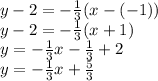Question

Find the equation of the normal to the curve y=x^2-2x^2-4x+1 at thepoint (-1,2)​

Answer 1

`y=-(1)/(3)x+(5)/(3)`

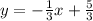
Explanation:

Assuming that the first exponent in the formula for the curve should be 3, not 2...

`y=x^3-2x^2-4x+1`

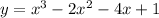
The derivative is

`y'=3x^2-4x+4`

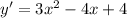
The slope of the tangent line at the point (-1, 2) is the value of the derivative at x = -1.

`y'|_(x=-1) = 3(-1)^2-4(-1)+4=3-4+4=3`

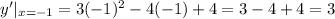
The slope of the normal line is the opposite reciprocal of the slope of the tangent line.

`m_{\text{normal} = -(1)/(3)`

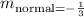
Using the Point-Slope form of a linear equation, the normal line is

`y-2=-(1)/(3)(x-(-1))\\y-2=-(1)/(3)(x+1)\\y=-(1)/(3)x-(1)/(3)+2\\y=-(1)/(3)x+(5)/(3)`