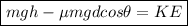Question

A box of mass m is initially at rest at the top of a ramp that is at an angle with the horizontal. The block is at a height h and length L

from the bottom of the ramp. The block is released and slides down the ramp. The coefficient of kinetic friction between the block and

the ramp is u. What is the kinetic energy of the box at the bottom of the ramp?

Answer 1

Hi there!

We can use the work-energy theorem to solve.

Recall that:

`E_i = E_f`

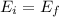
The initial energy equals the final energy (Conservation of Energy). However, we must take into account energy dissipated due to friction in this instance.

The energy lost due to friction is equivalent to the work done by friction. Recall the following:

• Normal force on an incline:
  `N = Mgcos\theta`
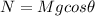
• Force due to friction:
  `F_f = \mu N = \mu mgcos\theta`

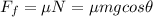
The work due to a force is:

`W = F \cdot d \\`

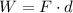
Since the displacement is in the same direction as the force, the dot-product becomes Fd.

The work due to friction then becomes:

`W_f = \mu mgdcos\theta`
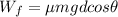
The work due to friction is SUBTRACTED from the initial potential energy.

Initial energy = GPE = mgh

Final energy = KE

Therefore:

`\boxed{mgh - \mu mgdcos\theta = KE}`