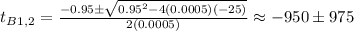Question

The readings, tA and tB, of two Celsius thermometers, A and B, agree at ice-point (0 oC) and steam point (100 oC), but elsewhere are related by equation tA = l + m tB + n tB 2 where l, m, and n are constants. When both thermometers are immersed in well-stirred oil bath, A registers 51 oC while B registers 50 oC. Determine the reading on B when A reads 25 oC

Answer 1

Step-by-step explanation:

From the case of well-stirred oil bath:

`51=l+50m+n(50^(2))\rightarrow 51=l+50m+2500n`

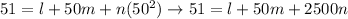
At the ice point, both of the thermometers show the same scale:

`0 = l + m(0) + n(0^(2)) \rightarrow l = 0`

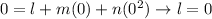
At the steam point, again, both of the thermometers show the same scale:

`100 = 0 + m(100)+n(100^(2)) \rightarrow 100 = 100m + 10000n \rightarrow 1 = m + 100n`

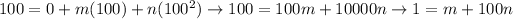
By eliminating those equations, we find:

`51=50(1-100n)+2500n \rightarrow 51=50-500n+2500n \rightarrow 1 = 2000n`

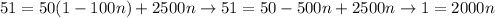
so we can obtain that:
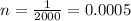`n=(1)/(2000)=0.0005` and
`m=1-100(0.0005)=1-0.05=0.95`

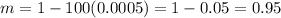
Now, we have the complete description of the relation between A and B scale as:
`t_(A)=0.95t_(B)+0.0005t_(B)^(2)`

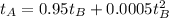
So, for
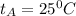`t_(A)=25^(0)C`:

`25 = 0.95t_(B)+0.0005t_(B)^(2) \rightarrow 0.0005t_(B)^(2)+0.95t_(B)-25=0`

`t_(B)_(1,2)=\frac{-0.95\pm\sqrt{0.95^(2)-4(0.0005)(-25)}}{2(0.0005)}\approx-950\pm975`

`t_(B)_(1)=25^(0)C \vee t_(B)_(2)=-1925^(0)C`